Making Good Decisions under Limited Information: Distortion-Information Tradeoffs in Social Choice and Matching
Short Biography
Aris Filos
-Ratsikas is an Assistant Professor at the University of Liverpool. He works on algorithmic mechanism design and algorithmic game theory, in particular mainly algorithmic mechanism design without money, social choice theory, divisible and indivisible item allocation and markets as well as fair division and the complexity of related problems.
He obtained his PhD degree from the Computer Science Department of Aarhus University, Denmark in 2015, under the supervision of Peter Bro Miltersen. In the past, he was a postdoctoral researcher at École polytechnique fédérale de Lausanne, at the Artificial Intelligence Laboratory led by prof. Boi Faltings and before that, he was a postdoctoral research assistant at the University of Oxford, at the Game Theory group led by prof. Elias Koutsoupias. His MSc advisor was prof. Ioannis Caragiannis.
Abstract of the Seminar
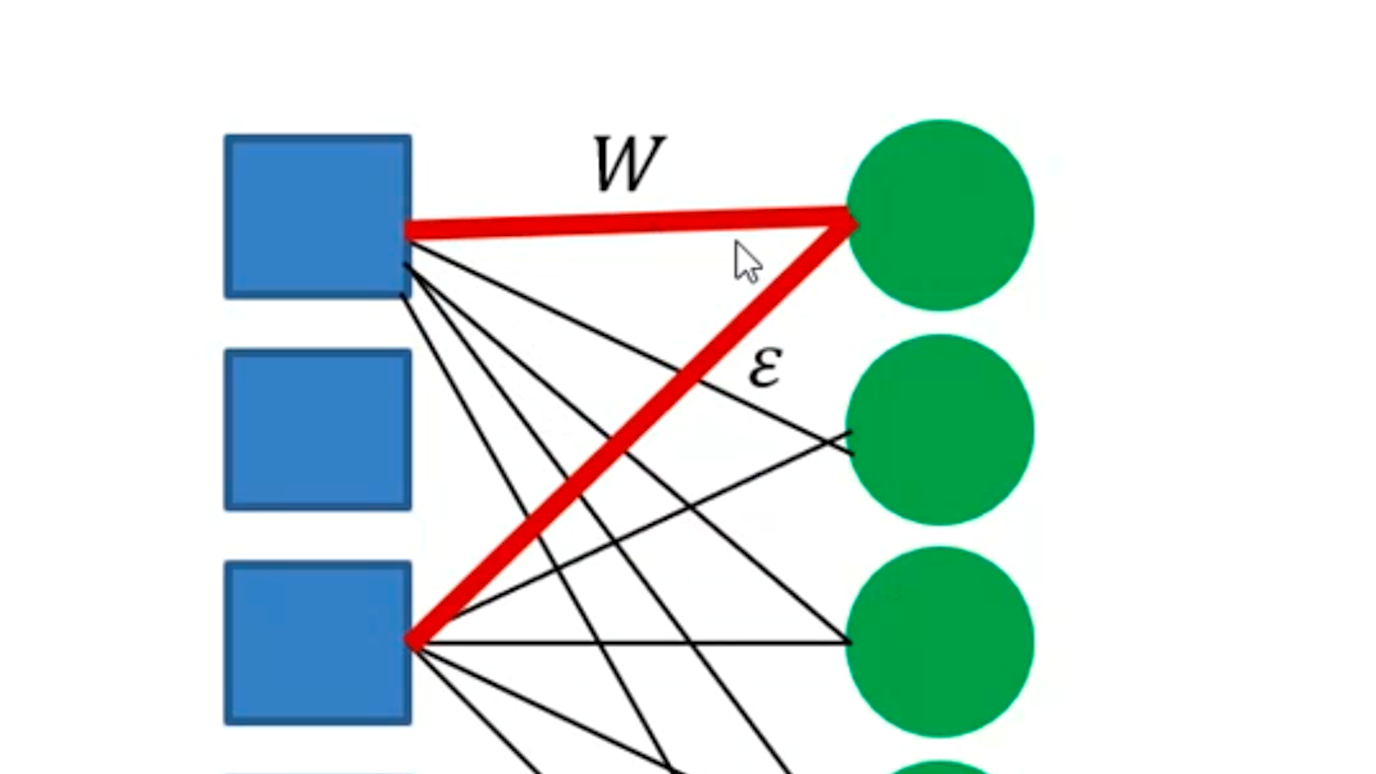
Aggregating the preferences of individuals into a collective decision is the core subject of study of social choice theory. In 2006, Procaccia and Rosenschein considered a utilitarian
social choice setting, where the agents have explicit numerical values for the alternatives, yet they only report their linear orderings over them. To compare different aggregation mechanisms, Procaccia and Rosenschein introduced the notion of distortion, which quantifies the inefficiency of using only ordinal information when trying to maximize the social welfare, i.e., the sum of the underlying values of the agents for the chosen outcome. Since then, this research area has flourished and bounds on the distortion have been obtained for a wide variety of fundamental scenarios. However, the vast majority of the existing literature is focused on the case where nothing is known beyond the ordinal preferences of the agents over the alternatives. We take a more expressive approach, and consider mechanisms that are allowed to further ask a few cardinal queries in order to gain partial access to the underlying values that the agents have for the alternatives. With this extra power, we design new deterministic mechanisms that achieve significantly improved distortion bounds and, in many cases, outperform the best-known randomized ordinal mechanisms. We consider both the setting of general social choice and one-sided matching, and provide bounds on the possible tradeoffs between the distortion and the amount of information elicited.