Modelling the spread of infectious deceases has always been an active research field but the current pandemic has put this area under a spotlight.
This motivated Dr. Vadim Shcherbakov and his colleague Dr. A. Gairat (Numerix, Moscow) to work on their joint paper Spread of infection on homogeneous trees.
The paper concerns a simple probabilistic model for the spread of infections in a homogeneous population. A population is modelled by a collection of sites representing individuals.
A site can be either susceptible to infection, or infected, or recovered and immune.
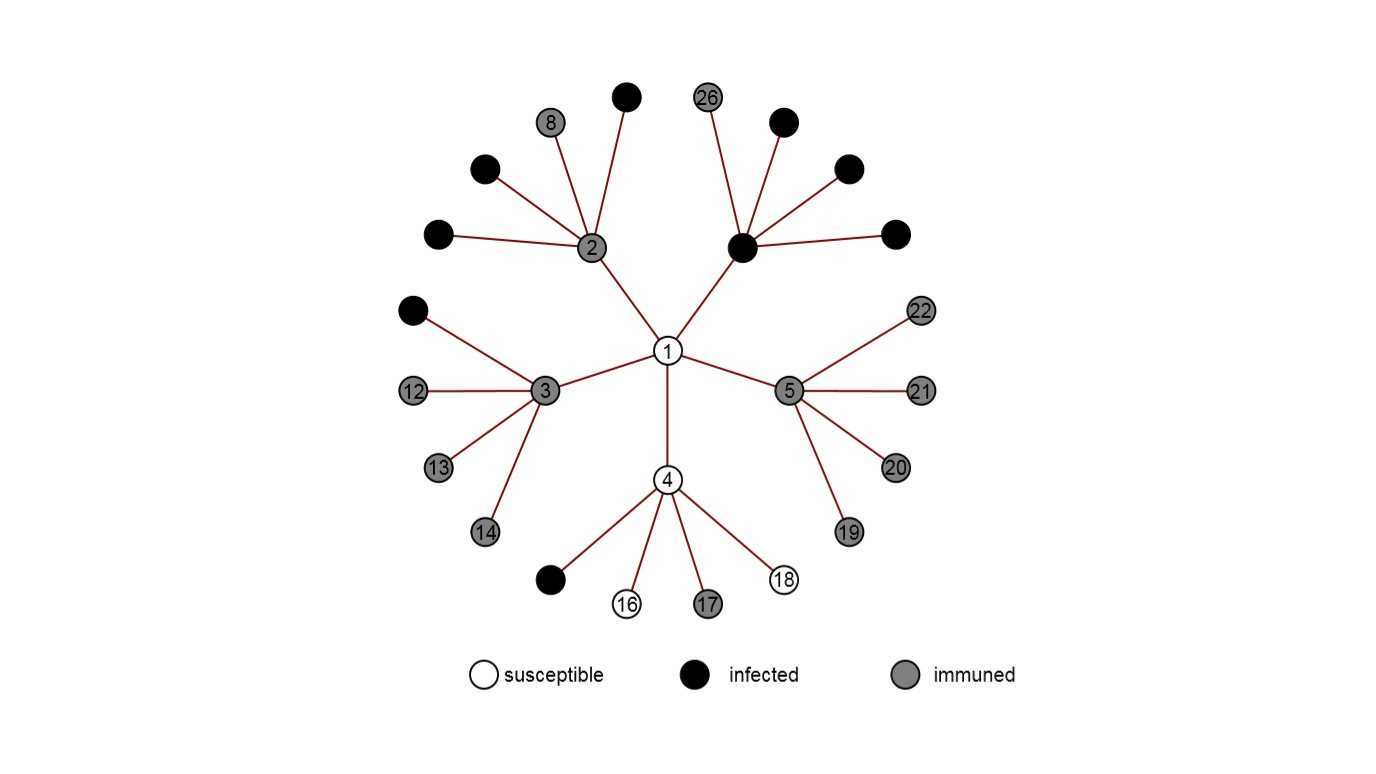
Each site has a fixed constant number of neighbours (homogeneity). The figure above illustrates the vicinity of a site labelled 1 and its neighbours labelled 2,3,4,5 and 6, where each site has 5 neighbours. A susceptible site becomes infected at the rate proportional to the number of infected neighbours and recovers later independently of the others.
Dr. Shcherbakov and Dr. Gairat show that the probability of the event that a site is still susceptible at a certain time moment is expressed in terms of a solution of the well-known Bernoulli differential equation.
Another interesting result is that, under an appropriate scaling, the probabilistic model of interest implies the differential equations of the classic SIR model. The latter is the main basic model used in epidemiology for modelling the spread of infections.
The mathematical results of the paper predict and confirm the most important features of the spread of real infections.
For example, the figure below illustrates how the number of social contacts (the parameter n) affects the probability of the event that at a certain time moment an individual is still not infected.

One can see that this probability decreases much faster as the number of contacts increases. In other words, measures of social distancing do matter!