Relaxing the independence assumption in optimization under uncertainty
Abstract:
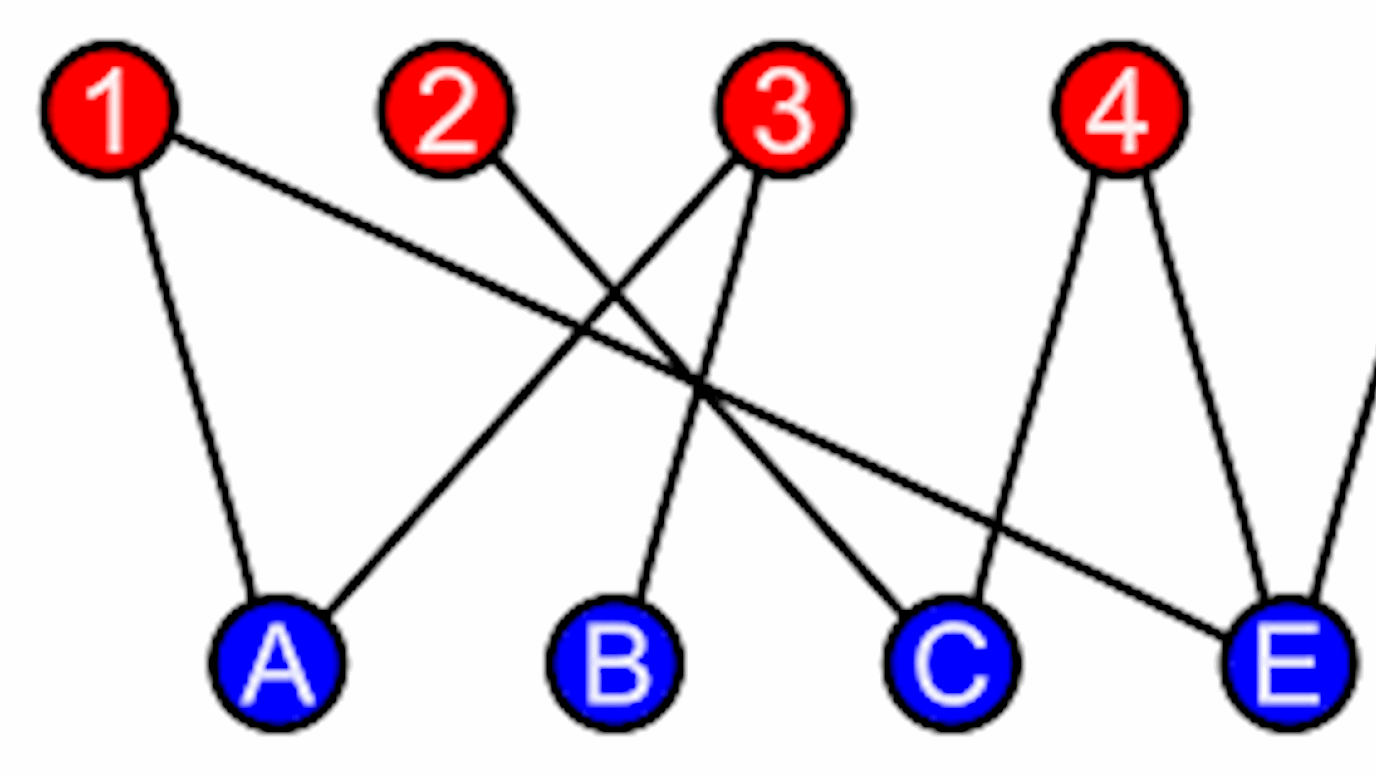
We reexamine three classical settings of optimization under uncertainty, which have been extensively studied in the past, assuming that the several random events involved are mutually independent. Here, we assume that such events are only pair-wise independent; this gives rise to a much richer space of instances. Our aim has been to explore whether positive results are possible even under the more general assumptions. We show that this is indeed the case. Indicatively, we show that, when applied to pair-wise independent distributions of buyer values, sequential posted pricing mechanisms get at least 1.299 of the revenue they get from mutually independent distributions with the same marginals. We also adapt the well-known prophet inequality to pair-wise independent distributions of prize values to get a 1/3-approximation using a non-standard uniform threshold strategy. Finally, in a stochastic model of generating random bipartite graphs with pair-wise independence on the edges, we show that the expected size of the maximum matching is large but considerably smaller than in Erdős-Renyi random graph models where edges are selected independently. Our techniques include a technical lemma that might find applications in other interesting settings involving pair-wise independence.
Based on joint work with Nick Gravin, Pinyan Lu, and Zihe Wang